![]() 上师大附属第二外国语学校
上师大附属第二外国语学校
第一学期第二次月考
高中一年级数学试题
1、填空题(本大题满分36分,共有12题)
1、已知集合![]() ,集合
,集合![]() ,那样
,那样![]() =________
=________
2、“![]() ”是“
”是“![]() ”的_____________条件
”的_____________条件
3、函数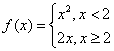 ,且
,且![]() ,则
,则![]() 的值是_______
的值是_______
4、若集合![]() ,则实数
,则实数![]() 的值是______
的值是______
5、函数![]() 的概念域为_________
的概念域为_________
6、集合![]() ,
,![]() ,若
,若![]() ,则实数
,则实数![]() 的范围是_____
的范围是_____
7、若函数![]() 是偶函数,且在
是偶函数,且在![]() 上单调递减,则
上单调递减,则![]() 的大小关系是______
的大小关系是______
8、函数![]() 是__________函数(填奇偶性)
是__________函数(填奇偶性)
9、函数![]() ,
,![]() 的最小值为______
的最小值为______
10、奇函数![]() 在
在![]() 上的表达式是
上的表达式是![]() ,则在
,则在![]() 上的
上的![]() 的表达式是_________
的表达式是_________
11、若函数![]() 是奇函数,则实数
是奇函数,则实数![]() 的值为_____
的值为_____
12、概念在![]() 上的偶函数
上的偶函数![]() 在
在![]() 上的图像如图所示,
上的图像如图所示,
则不等式![]() 的解集是_______
的解集是_______
2、选择题(共4小题,每题4分)
13、假如![]() ,那样下列不等式中错误的是( )
,那样下列不等式中错误的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
14、在下列四组函数中,两函数表示同一函数的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
15、设集合![]() ,则集合
,则集合![]() 的真子集的个数为( )
的真子集的个数为( )
A、3 B、7 C、8 D、16
16、下列四个函数中,则![]() 上为增函数的是( )
上为增函数的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、解答卷(共5小题,共48分)
17、(本题满分8分)已知集合![]() ,
,![]() ,求
,求![]()
18、(本题满分8分)若函数![]() 的概念域为
的概念域为![]() ,求实数
,求实数![]() 的取值范围
的取值范围
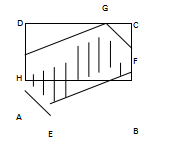
19、(本题满分10分)如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知![]() ,
,![]() ,且
,且![]() ,设
,设![]() 绿地面积为
绿地面积为![]()
(1)写出![]() 关于
关于![]() 的函数关系式,并指出这个函数的概念域
的函数关系式,并指出这个函数的概念域
(2)当![]() 为什么值时,绿地面积
为什么值时,绿地面积![]() 最大?
最大?
20、(本题满分10分)已知![]() ,
,![]() ,
,![]() 。
。
(1)求函数![]() 的概念域并画出
的概念域并画出![]() 的图像
的图像
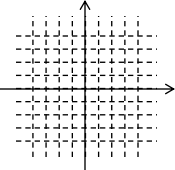 (2)写出函数
(2)写出函数![]() 的单调区间
的单调区间
21、(本题满分12分)已知函数![]() 是概念在
是概念在![]() 上的增函数,且
上的增函数,且![]()
(1)求![]() 的值
的值
(2)若![]() ,解关于
,解关于![]() 不等式
不等式![]()







